Epäintuitiivinen äärettömyys?

Tänään, hyvät ihmiset, kokeilen tieteen popularisointia – tarkalleen ottaen matematiikan popularisointia. Kohdeyleisöni olette te, joten pyrkimykseni on kirjoittaa tekstiä, jota ymmärrätte. Antakaa minulle mahdollisuus! Aiheeseen liittyy hyvin vähän laskennallisuutta, ja tekstin seassa on paljon kuvia! Kyse on enemmän ideoista, kuten matematiikassa yleensäkin. Laskeminen jätetään insinööreille.

Huomautettakoon myös, että tekstin pituutta ei tule pelästyä, sillä nimenomaan se, että selittää asioita ymmärrettävästi, tuottaa pituutta. Jos jättää asioita kirjoittamatta, voi saada aikaan hyvin lyhyen tekstin, jota kukaan ei tajua.

\(\newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}}\)

Johdanto

Vierailin kesällä 2016 Maunulassa Helsingin matematiikkalukion tapahtumassa Matematiikan yö, jossa keksin yhden kysymyksen mystiseen ”pizzakisaan”. Vastauksen kysymykseen oli tarkoitus olla joko ”totta” tai ”epätotta” (eli kysymykset olivatkin oikeastaan väittämiä).* Keksimäni kysymys (tai siis väite) oli seuraavanlainen:

Parillisia kokonaislukuja on vähemmän kuin kaikkia kokonaislukuja.

Saattoi se kyllä olla parittomiakin eikä parillisia, enhän minä niin tarkkaan muista. Vastaukseni väitteeseen on joka tapauksessa ”epätotta”, eli parillisia on ihan yhtä paljon kuin kaikkia kokonaislukuja yhteensä. Yllättikö vastaus sinut, rakas lukijani? Jos yllätti, jatka toki lukemista. Ja jos ei, niin jatka silti, ehkä yllätyt jostain muusta. Tai jos et halua yllättyä, sekin on ihan fine.

Kokonaislukuja – siis nolla (\(0\)), positiiviset kokonaisluvut (\(1, 2, 3, \dots\)) sekä negatiiviset kokonaisluvut (\(-1, -2, -3, \dots\)) yhdessä – näyttäisi olevan tiheämmässä kuin parillisia kokonaislukuja (\(\dots, -4, -2, 0, 2, 4, \dots\)), ja siksi tuntuisi, että parillisia kokonaislukuja olisi selkeästi vähemmän kuin kaikkia kokonaislukuja. Eihän se niin voi mennä, että jos luvuista otetaan puolet pois, niin jäljellä on yhtä paljon kuin oli aiemmin, eihän?! Mutta edelleen väitän, että vaikka se saattaakin kuulostaa näin ensialkuun epäintuitiiviselta, näin asia on (tai niin sen pitäisi olla; matematiikassa on se hauska puoli, että määritelmät saa itse päättää). Yritän myös tässä tekstissä perustella väitteen.

Opetellaan laskemaan

Me emme osaa – ainakaan vielä – laskea. Emme, jos äärettömyyksiä on mukana. Mitä on ääretön plus yksi? Ääretön plus kaksi? Mitä edes on ääretön? Olemme tällä hetkellä kuin esikoululaisia, jotka eivät vielä ihan osaa laskea sataan asti.

Puhutaanpa joukoista. Siitä tässä on kyse, joukoista ja niiden kokojen vertailusta. Joku voisi jopa sanoa, että joukko-oppi – matematiikan osa-alue, joka tutkii, yllättävää kyllä, joukkoja – on oikeastaan äärettömyyden tutkimista. Mikä on joukko? Joukko on, naiivisti ajateltuna, kokoelma jotain otuksia. Sanotaan nyt vaikka, että mikä tahansa kokoelma mitä tahansa otuksia.** Niitä otuksia kutsutaan joukon alkioiksi. Muuta ei tässä yhteydessä tarvita.

Ennen kuin osaamme laskea, kuinka vertailisimme kahden eri joukon kokoa? Mietitään ihan äärellisiä joukkoja nyt. Jos vaikkapa \(A\) on joukko turkooseja palloja ja \(B\) on joukko punaisia palloja (ks. kuva 1), miten voimme selvittää, onko niissä sama vai eri määrä palloja?

Ensimmäinen ajatus olisi varmaan laskea, montako palloa on joukossa \(A\) ja montako joukossa \(B.\) Mutta entä, jos ei osata laskea? Miten lapsi, joka ei vielä osaa laskea viiteen, asian ratkaisisi?

Jollekulle saattaisi tulla mieleen, että hei, ryhmitellään joukkojen alkiot (eli jäsenet) pienemmiksi joukoiksi, joiden alkioiden lukumäärä osataan laskea. Jos esimerkiksi osataan laskea jo kolmeen, niin voidaan ryhmitellä isomman joukon alkioita kolmen ryhmiin ja sitten laskea, montako ryhmää on, jos niitä on tarpeeksi vähän – mutta jos ei, niin pitäisi ryhmitellä ryhmiä; alkaa mennä monimutkaiseksi. Hups, ehkä lapsi, joka ei osaa vielä laskea kuin kolmeen, ei tekisikään noin. Toki kuvan 1 tilanne on hyvin yksinkertainen, mutta jos palloja olisi todella enemmän kuin viisi, lapsi olisi ongelmissa.

No miten sitten? Miten selvitämme, onko punaisia palloja yhtä paljon kuin turkooseja ilman, että ratkaisuun sisältyy mitään laskemista? En tiedä, ratkaisisiko lapsi oikeasti ongelmamme näin, mutta helppo tapa on laittaa pallot vierekkäin ja katsoa, riittääkö jokaiselle turkoosille pallolle punainen pari.*** Jos riittää, palloja on kummassakin joukossa yhtä paljon, ja jos ei riitä, niitä on enemmän, joita jäi yli. Tässä äärellisessä tapauksessa suhteellisen selvää, eikö?

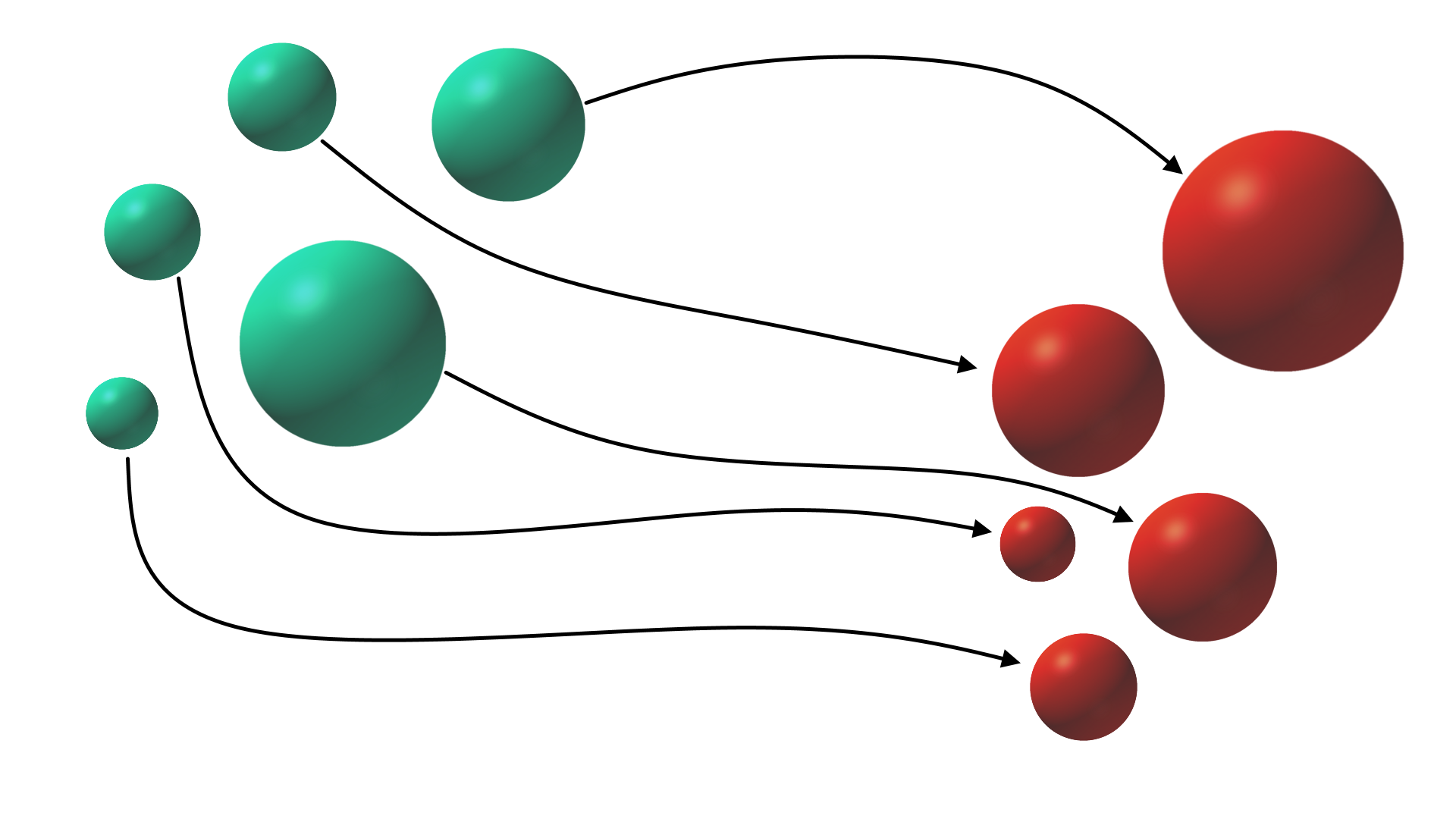
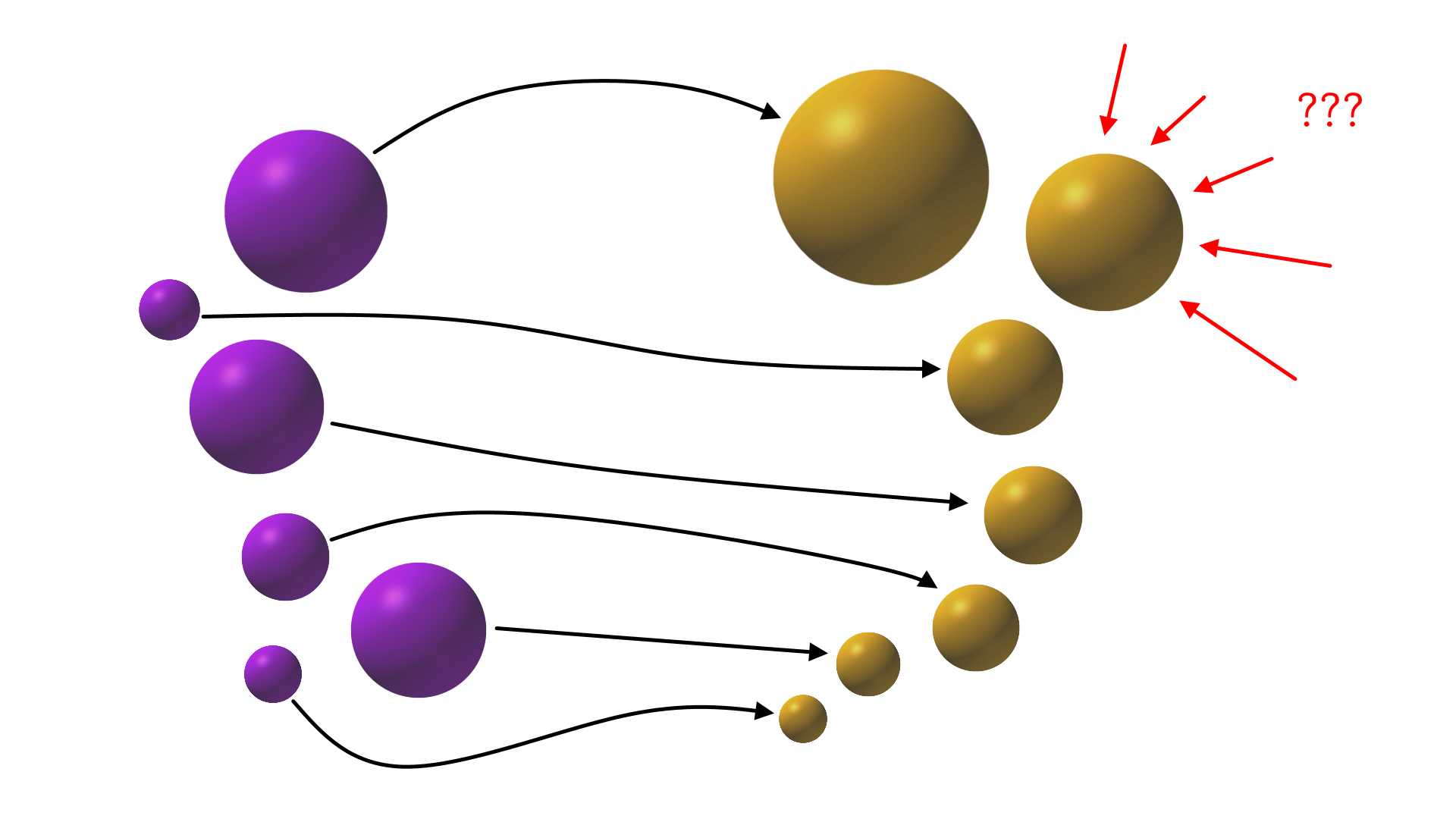
Tämä on se periaate, jonka haluamme yleistää myös äärettömille joukoille. Kaksi ääretöntä joukkoa \(A\) ja \(B\) ovat ”samankokoiset” (matemaatikot sanovat, että joukot ovat yhtä mahtavat), jos (ja vain jos) on olemassa bijektio joukosta \(A\) joukkoon \(B\).

”Hetkinen! Nyt putosin kärryiltä!” saatat tuumata. Mikä kumma on bijektio? Okei, tämä on aika tärkeää, joten yritän selittää. Jos koulumatematiikasta on jo pitkä aika, niin funktion käsite saattaa olla hieman hukassa. Itse asiassa sanalla ”funktio” saattaa olla negatiivinen konnotaatio, jos ei sattunut tykkäämään funktioista koulumatematiikassa. Käytänpä siis toista sanaa: kuvaus. Kahden joukon, sanotaan \(A\) ja \(B\), välinen kuvaus, olkoon vaikka \(k\) niin kuin kuvaus, on sellainen (konemainen) otus, joka raksuttaa sisäänsä joukon \(A\) alkioita, oms noms, ja sylkee ulos joukon \(B\) alkioita. Lisäksi se tekee sen vielä niin, että jokaisella joukon \(A\) alkiolla on yksikäsitteinen kuva eli jos \(a\) on joukon \(A\) alkio, niin kuvaus \(k\) liittää siihen jonkin yhden ja ainoan otuksen \(b\), joka kuuluu joukkoon \(B\). Tätä voi havainnollistaa helposti kuvalla, jopa useammalla – ja ehkä niin on parasta, sillä en koe tehneeni hirveän hyvää työtä selittämisessä.

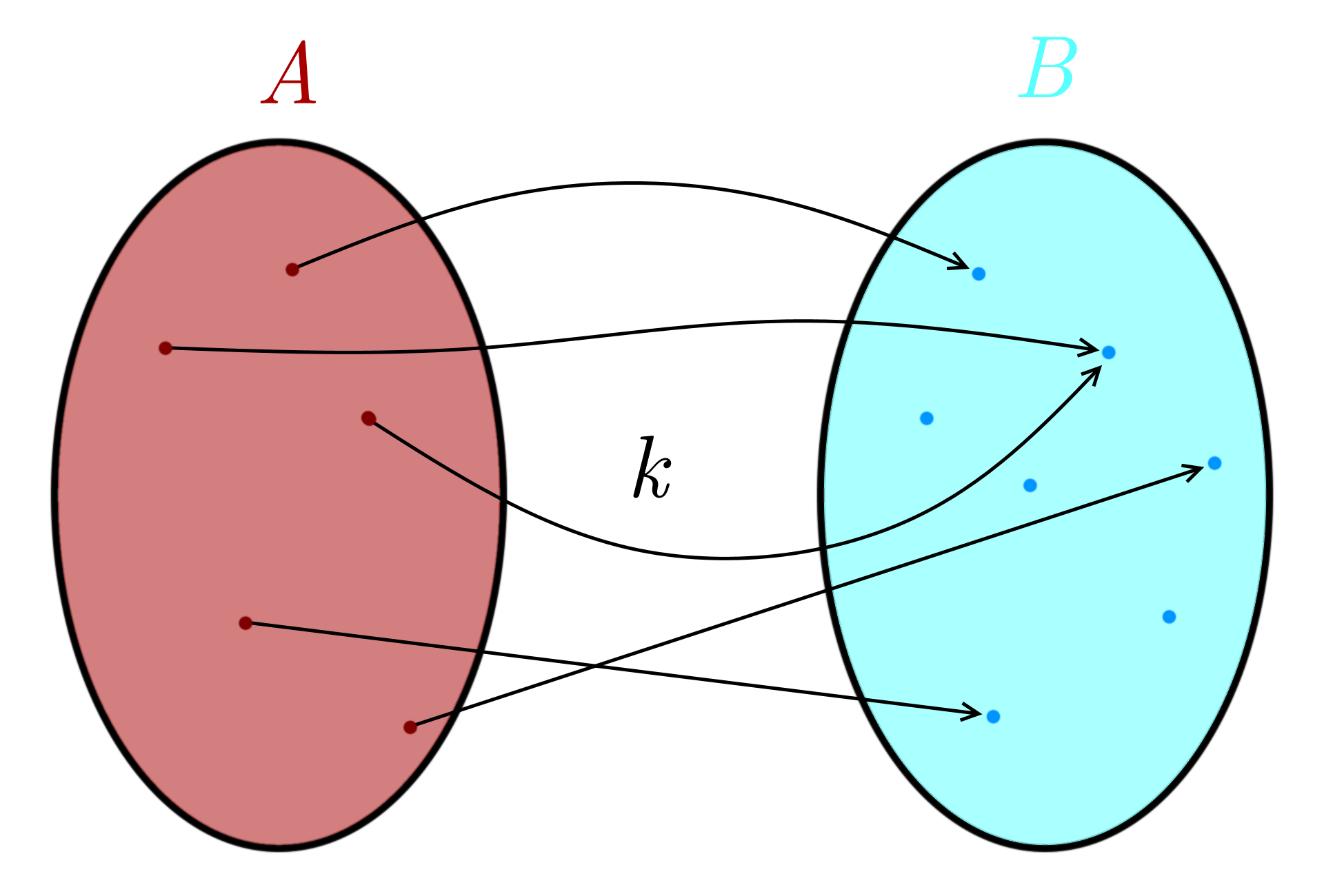
Kuvissa 4 ja 7 on kuvaus. Kuvat 5 ja 6 taas ovat esimerkkejä… ööh ei-kuvauksista. Eli epäesimerkkejä – tätä kuvaus ei ole. Oleellista on se, että kuvissa 4 ja 7 lähtöjoukon (\(A\)) jokaisesta alkiosta lähtee yksi nuoli – ja vain yksi. Kuva 5 epäonnistuu siinä, että yhdestä alkiosta lähteekin kaksi nuolta, ja kuva 6 epäonnistuu siinä, että yhdestä alkiosta ei lähde nuolta lainkaan. Maalijoukon (\(B\)) alkioihin saa mennä monta nuolta, eikä niihin kaikkiin ole pakko mennä nuolta laisinkaan. Lähtöjoukko on tosiaan siis se joukko, jonka alkioita muutetaan sen toisen joukon alkioiksi, ja ne, joiksi muutetaan, ovat maalijoukon alkioita; ihan loogisia nimiä, vai mitä? Lähtö ja maali. Jos \(a\) on joukon \(A\) alkio, niin sitä otusta, joksi \(k\) muuttaa \(a\):n, merkitään \(k(a)\) ja sanotaan alkion \(a\) kuvaksi, mikä lienee sekin ihan järkevää, jos miettii sanaa ”kuvaus”. Kuvaus kuvaa kuvattavan kuvaksi. Aika kuvaavaa.

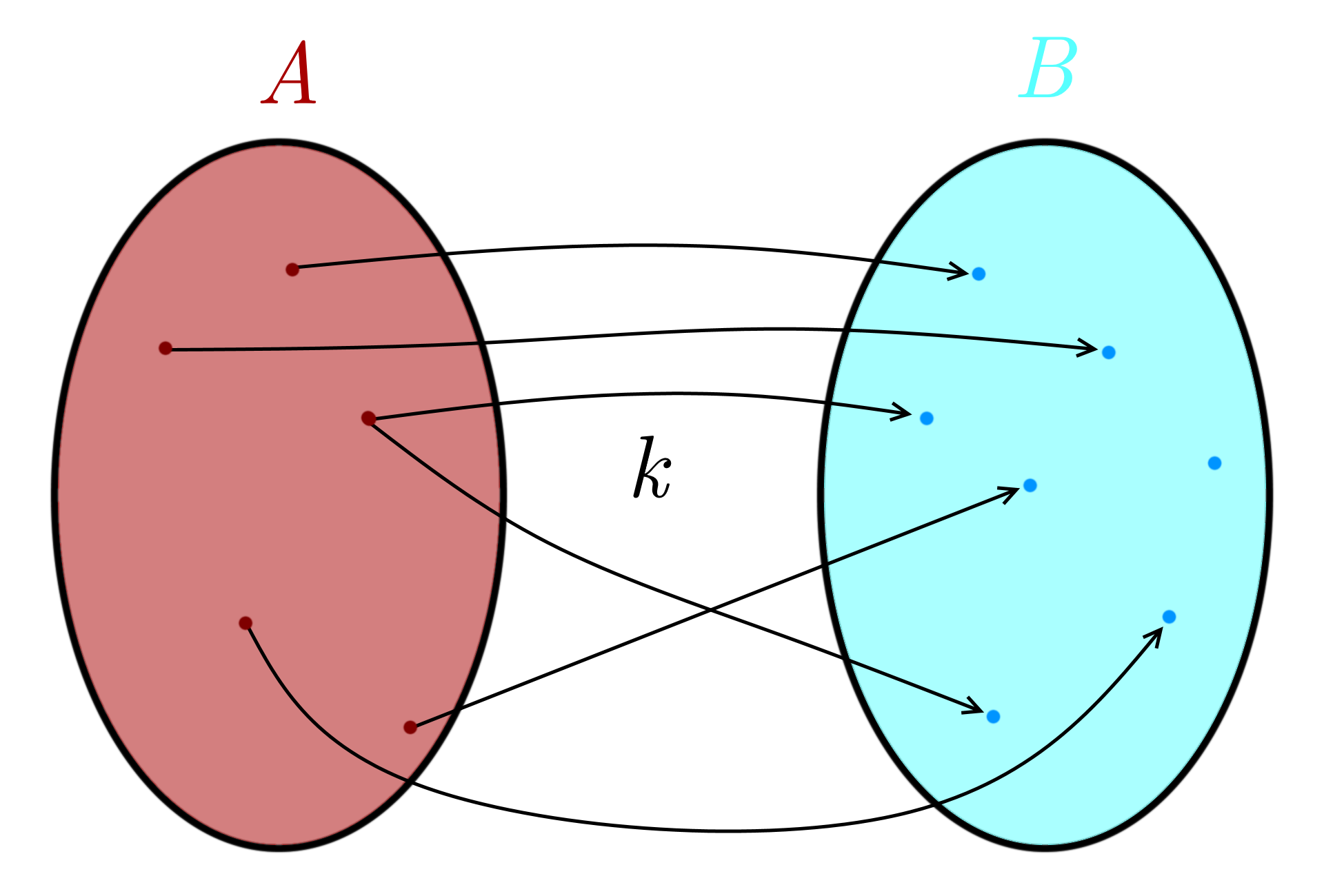
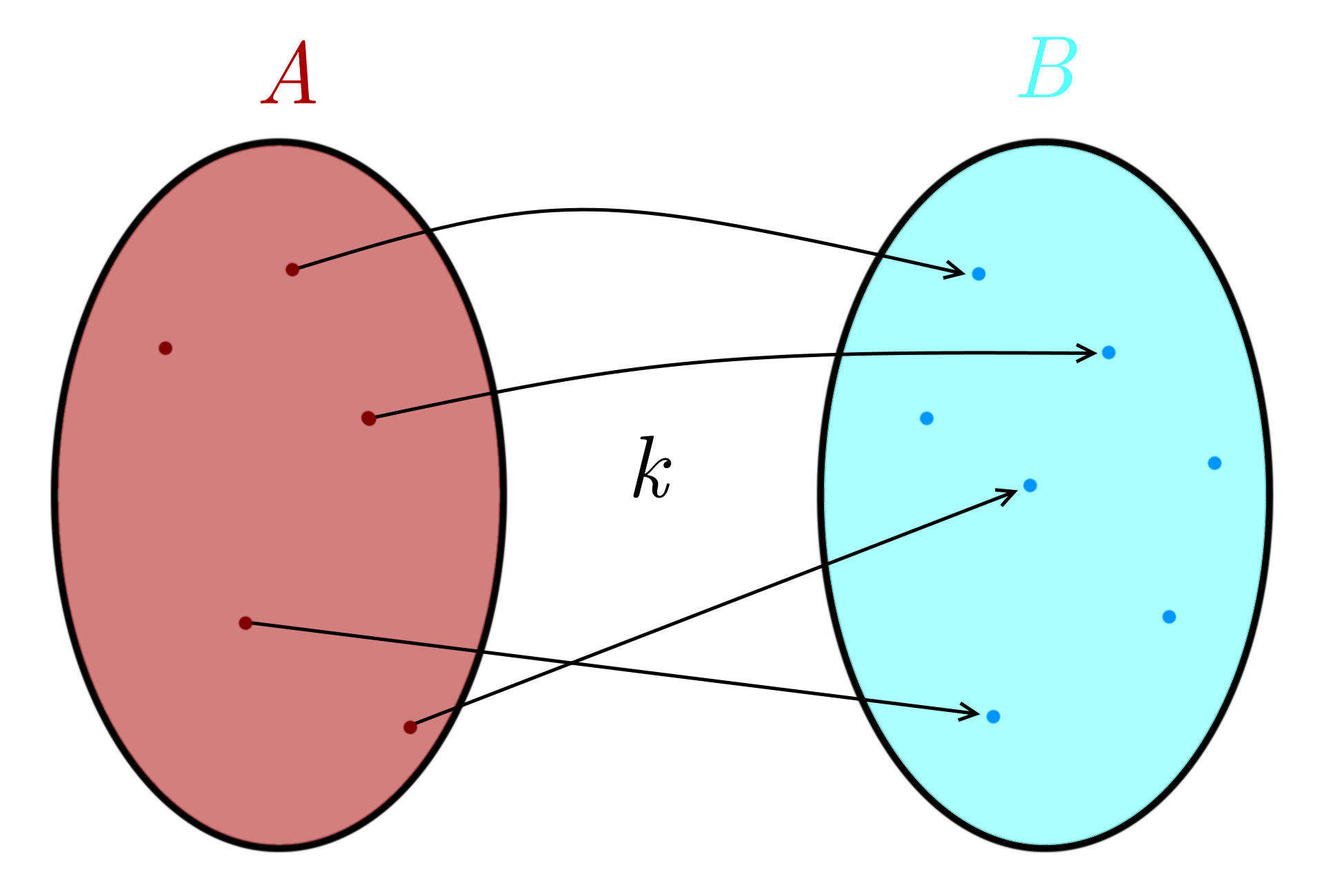
Okei, se bijektio. Bijektio joukkojen \(A\) ja \(B\) välillä on sellainen kuvaus, että jokaiseen joukon \(B\) alkioon myös liittyy täsmälleen yksi joukon \(A\) alkio. Tämä kuvaus siis ikään kuin parittaa joukkojen alkiot keskenään, se on yksi-yhteen-vastaavuus. Se on se pointti, mikä tästä on hyvä jäädä mieleen – bijektio on yksi-yhteen-vastaavuus. Kuvassa 2 on paritettu kuvan 1 pallot bijektiivisesti. Eli kuvassa bijektiivisyyden huomaa siitä, että jokaiseen maalijoukon alkioon tulee nuoli – ja vain yksi nuoli. Jos johonkuhun ei tule nuolta, niin kuvaus ei ole bijektio. Samoin, jos johonkuhun tulee kaksi nuolta, kyseessä ei ole bijektio. Kuvassa 7 on Vennin kaavio bijektiosta. Yksi hyvä tapa ajatella on, että kuvaus on bijektio, jos ja vain jos se on yhä kuvaus, kun nuolien suunnat kääntää takaperin; nämä bijektion ylimääräiset ominaisuudet kuvaukseen nähden ovat näes samoja ominaisuuksia, mitkä kuvaukselta vaadittiin mutta maali- eikä lähtöpuolella.

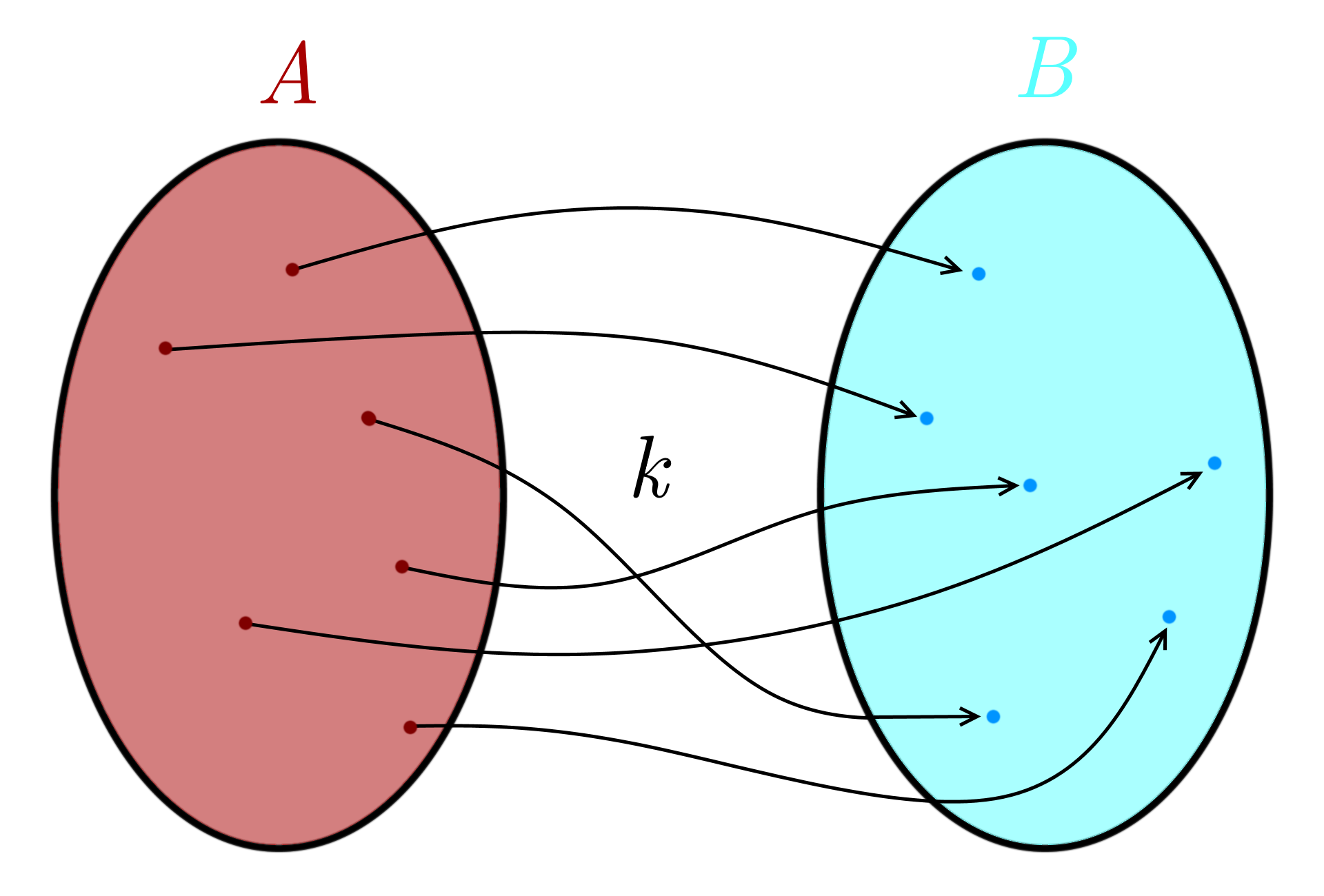
Mainitsin, että kaksi joukkoa ovat yhtä mahtavat, jos on olemassa bijektio niiden välillä, siis yksi-yhteen-vastaavuus. Siksihän näistä ruvettiin puhumaan. No okei, miksi tässä on järkeä? Tai siis onhan siinä, kun miettii sitä äärellistä esimerkkiä. Kahdessa joukossa on saman verran alkioita, jos ne voidaan laittaa vierekkäin ja yhtään ei jää yli. Mutta minä menen vielä pidemmälle! Minä väitän, että laskeminen ei ole mitään muuta kuin asioiden laittamista yksi-yhteen-vastaavuuteen tietyn lukujoukon kanssa! Esimerkiksi jos minulla on viisi omenaa, niin niiden laskeminen on sama asia kuin jos muodostaisin bijektion niiden omenoiden joukolta joukolle \(\{ 1, 2, 3, 4, 5 \}\).

Mitä ihmettä? Nyt kuulostaa jo aika abstraktilta. Mutta ei, antakaa, kun selitän. Otetaan esimerkiksi jokin joukko symboleita, sanotaan vaikka nuo, mitkä ovat kuvassa 8. En kirjoita symboleita lähtökohtaisesti mihinkään järjestykseen, jotta järjestys ei sumenna esimerkin tarkoitusta (lisäksi valitsin symbolit niin, että ne eivät ole samasta aakkostosta, jotta niiden tavallinen sanakirjajärjestys ei sotke mielikuvia).

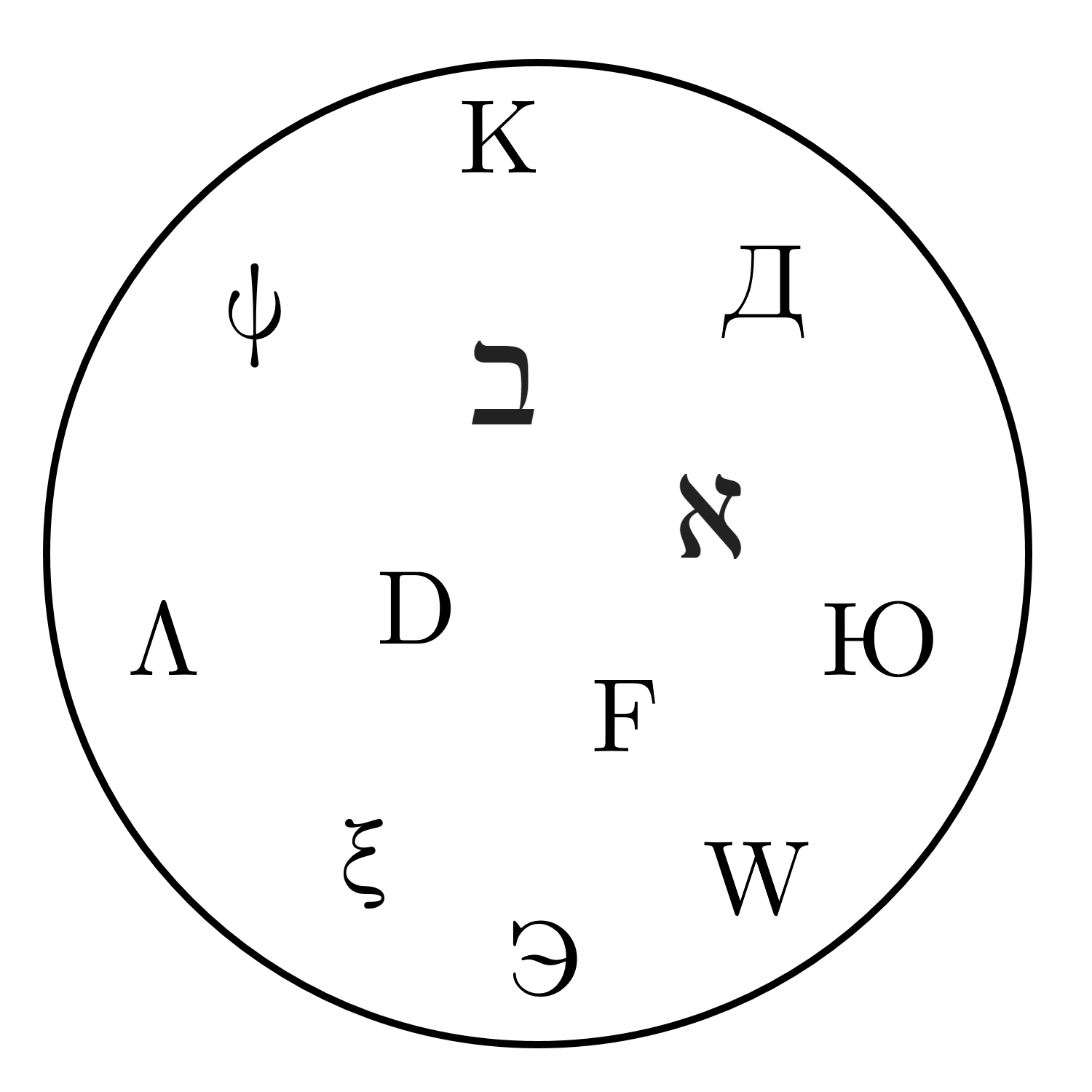
Okei. Meillä on epämääräinen kasa jotain symboleita, joista osa on latinalaisia, osa kreikkalaisia ja osa kyrillisiä kirjaimia, ja pari heprealaistakin siellä on. No mitäs sitten? Sitten lasketaan ne.

1. K,
2. ψ,
3. Λ,
4. ב,
5. D,
6. Д,
7. א,
8. Ю,
9. F,
10. ξ,
11. W,
12. Э.

Nyt ne on laskettu, niitä oli kaksitoista. Mutta hetkinen nyt, muodostin listan, jossa jokaista lukua \(1, \dots, 12\) vastaa yksi ja vain yksi symboli eli kirjoitin yksi-yhteen-vastaavuuden! Pohjimmiltaan kyse on siis täysin samasta asiasta, ja siksi on luonnollista lähteä yleistämään tätä periaatetta myös äärettömille joukoille; jos ne voidaan parittaa, niitä on yhtä paljon.

Vastaus kysymykseen

Mietitäänpä sitten niitä kokonaislukuja. Kokonaislukujen joukkoa merkittäköön symbolilla \(\Z\). Olkoon \(2\Z\) parillisten kokonaislukujen joukko. Määritellään \(f\) olemaan sellainen kuvaus joukosta \(\Z\) joukkoon \(2\Z\), että sille pätee \(f(n)=2n\) jokaisella kokonaisluvulla \(n\), eli toisin sanoen kuvaus \(f\) kaksinkertaistaa jokaisen kokonaisluvun, joka sille syötetään. Se on bijektio kokonaislukujen ja parillisten kokonaislukujen välillä, sillä jokaiseen kokonaislukuun \(n\) liitetään (yksikäsitteinen) parillinen kokonaisluku \(2\cdot n\) ja toisaalta jokaiseen parilliseen kokonaislukuun \(m\) kuvaus \(f\) liittää kokonaisluvun, josta saadaan \(m\) kertomalla kahdella (siis luku on \(m/2\) ja se on yksikäsitteinen niin kuin kuuluukin). Esimerkiksi siis \(f(1)=2\) ja \(f(35)=70\), ja jos valitaan jokin satunnainen parillinen kokonaisluku, vaikkapa \(42\), niin huomataan, että \(42=f(21)\), sillä \(2\cdot 21 = 42\). Tämä osoittaa, että kokonaislukuja ja parillisia kokonaislukuja on yhtä paljon: ne voidaan parittaa. Vielä havainnollisempi lista alla:

\(\qquad\vdots\)
\(-3\mapsto -6\)
\(-2\mapsto -4\)
\(-1\mapsto -2\)
\(\phantom{-}0\mapsto\phantom{-}0\)
\(\phantom{-}1\mapsto\phantom{-}2\)
\(\phantom{-}2\mapsto\phantom{-}4\)
\(\phantom{-}3\mapsto\phantom{-}6\)
\(\qquad\vdots\)

Vastaava bijektio löytyy kokonaislukujen ja parittomien kokonaislukujen välille, nimittäin kuvaus \(n\mapsto 2n+1\) (siis kuvaus, joka kertoo kokonaisluvun kahdella ja lisää siihen ykkösen). Lisäksi luonnollisten lukujen joukosta \(\N\) – joukosta, jossa ovat luvut \(0, 1, 2, \dots\) – löytyy bijektio kokonaisluvuille:

\(0\mapsto 0,\)
\(1\mapsto 1,\)
\(2\mapsto -1,\)
\(3\mapsto 2,\)
\(4\mapsto -2,\)
\(5\mapsto 3,\)
\(6\mapsto -3,\)
ja niin edelleen.

Voi vielä olla ihan helppo uskoa, että kokonaisluvut voidaan listata tuolla tavalla luonnollisilla luvuilla, mutta entäpä rationaaliluvut (eli murtoluvut)? Ha ha ha, minäpä väitän, että nekin voidaan listata samalla tavalla. Murtolukujakin on yhtä paljon kuin kokonaislukuja tai luonnollisia lukuja. Mutta miten tämä voisi pitää paikkansa? Jos katsotaan kahta rationaalilukua, niin niiden välistä löytyy aina rationaaliluku (keskiarvo nyt ainakin). Miten niitä voisi olla saman verran kuin kokonaislukuja, kun niitä on paljon, paljon tiheämmässä kuin kokonaislukuja??? Tosin samaa ajattelimme kokonaisluvuista ja parillisista luvuista, emmekö? Noh, joka tapauksessa väitteeni osoittamiseksi riittää löytää sopivanlainen paritus (shippaus?).

Yksinkertaisuuden vuoksi annan vastaavuuden vain positiivisille rationaaliluvuille. Kuvassa 9 on taulukoitu positiiviset rationaaliluvut. Kuvassa 10 taas on havainnollistettu, miten tämän taulukon voi käydä läpi niin, että saadan vastaavuus luonnollisten lukujen kanssa.

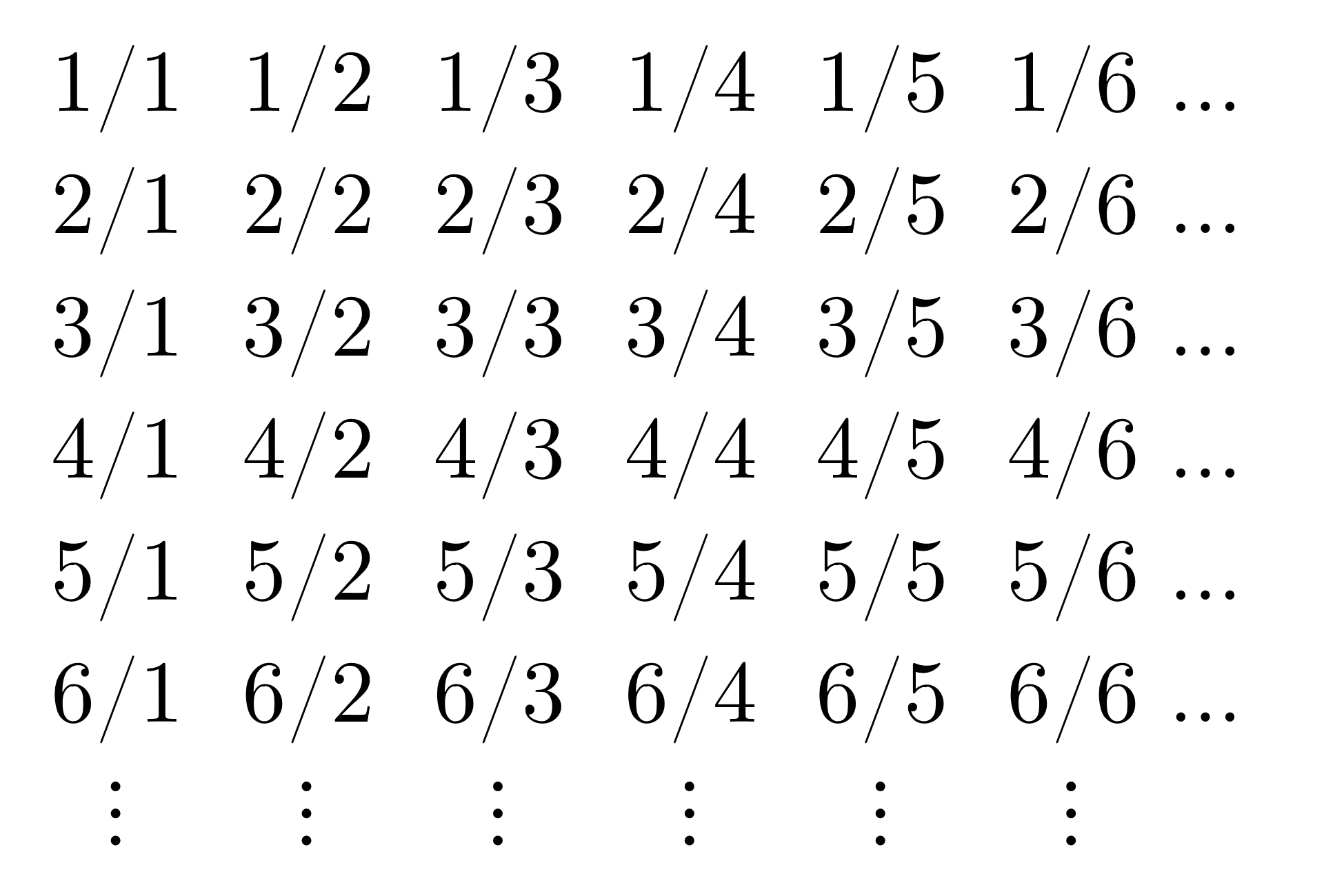
Eli lista alkaa \(1/1, 1/2, 2/1, 3/1, 2/2, \dots\). Tarkkaavainen lukija saattaa huomata, että taulukossa sama luku saattaakin esiintyä useamman kuin yhden kerran. Esimerkiksi \(1/2 = 2/4 = 3/6 = \dots\), joten jotkin luvut (itse asiassa kaikki) tulevat numeroiduksi useampaan kertaan (äärettömän moneen). Tämä ei haittaa, sillä voidaan osoittaa, että jos jokin joukko voidaan tällä tavalla ”peittää” toisen joukon alkioilla, niin tämä peittävä joukko on ”vähintää yhtä mahtava” kuin peitettävä joukko. Jätän näiden väitteiden täsmällisen muotoilun sikseen. Pointti kuitenkin on, että tällä tavalla nähdään, ettei rationaalilukuja ole ainakaan enempää kuin luonnollisia lukuja, sillä ne voidaan listata. Lisäksi niitä on ääretön määrä, joten niitä on yhtä paljon. Proof by intimidation.

Mitä on ääretön?

No nyt saattaa herätä kysymys, että onko sitten kaikissa äärettömissä joukoissa yhtä paljon kamaa. Ja se voi aluksi tuntua ihan järkevältä ajatukselta, eikö? Ääretön on ääretön, vai mitä? Huomautettakoon, että en ole missään vaiheessa kertonut, mitä ”ääretön” tarkoittaa. On melko luonnollista määritellä äärettömyys seuraavasti: joukko on ääretön, jos se ei ole äärellinen. Melko ilmiselvää, joo, mutta mitä tarkoittaa äärellisyys? Öh, no, yksi hyvä tapa määritellä äärellisyys on seuraava: joukko \(A\) on äärellinen, jos on olemassa jokin luonnollinen luku \(n\) ja bijektio joukolta \(\{0, 1, \dots, n-1\}\) joukolle \(A\). Eli käytännössä, joukko on äärellinen, jos siellä on jonkin äärellisen luvun verran alkioita. Kuulostaa melkein kehämääritelmältä, mutta noh, tietyllä tapaa luonnolliset luvut ovat äärellisten joukkojen arkkityyppejä. Joukko on äärellinen, jos on olemassa joku \(n\) siten, että siinä joukossa on \(n\) alkiota.

Okei, eli joukko on ääretön, jos millekään luvulle \(n\) ei löydy yhtäkään ainutta bijektiota, joka parittaisi luvut \(0, \dots, n\) joukon alkioiden kanssa. On syytä huomata, että äärellisten joukkojen tapauksessa jos jokainen lähtöjoukon alkio kuvataan eri kuva-alkioiksi eli jokainen lähtevä nuoli menee eri paikkaan, niin jos tällä tavalla ei saatu bijektiota, niin mitään bijektiota ei ole olemassa. Äärettömässä tapauksessa taas… jos jokin bijektioehdokas epäonnistuu parittamaan KAIKKI maalijoukon alkiot, se ei tarkoita, etteikö jollain muulla tavalla voitaisi parittaa lukuja. Esimerkiksi jos yritetään parittaa luonnolliset luvut (\(0, 1, 2, \dots\)) kokonaislukujen (\(\dots, -1, 0, 1, \dots\)) kanssa käyttämällä kuvausta, joka kuvaa jokaisen luvun itselleen, niin kyseessä ei ole bijektio, koska negatiivisille luvuille ei kuvaudu mitään. Mutta tästä ei seuraa, etteikö jokin bijektio olisi olemassa. Sen sijaan jos kuvaamme joukon \(\{0, 1\}\) joukolle \(\{-1, 0, 1\}\), niin mikään kuvaus ei voi onnistua parittamaan näitä joukkoja.

Vastatakseni aiempaan kysymykseen: ei, kaikissa äärettömissä joukoissa ei ole saman verran alkioita. Reaalilukujen joukossa (eli ”desimaalilukujen” joukossa), johon kuuluvat rationaalilukujen lisäksi esimerkiksi sellaiset luvut kuin \(\pi\), \(\sqrt{2}\) ja niin edelleen, on enemmän alkioita kuin luonnollisten lukujen joukossa. Tokihan luonnolliset luvut löytyvät reaalilukujen sisältä, sillä luvut \(0, 1, 2, \dots\) ovat reaalilukuja. Siten reaalilukuja on nyt ainakin yhtä paljon kuin luonnollisia lukuja. Mutta miksi niitä on enemmän? Miksemme voisi listata desimaalilukuja samalla tavalla kuin listasimme vaikkapa rationaaliluvut?

Kokeillaan! Yksinkertaisuuden vuoksi yritetään listata kaikki reaaliluvut lukujen \(0\) ja \(1\) väliltä. Jokainen tällainen desimaaliluku on muotoa \(0,x_1x_2x_3\dots\), missä jokainen \(x_i\) on jokin numero. Esimerkiksi \(0,12838658599383859836739390\). Jos desimaalikehitelmä päättyy, niin ajatellaan, että lopussa on ääretön määrä nollia. Nyt minä tosiaan väitän, että näitä lukuja on liikaa listattavaksi. Oletetaan hetki, että olen väärässä ja meillä onkin jokin tapa listata ne luvut. Lista voisi olla esimerkiksi seuraava:

1. \(0,1121121111111911\dots\)
2. \(0,1526374859607951\dots\)
3. \(0,9999299929939939\dots\)
4. \(0,0000000001000000\dots\)
5. \(0,2635454545545545\dots\)
6. \(0,1231231231231231\dots\)
7. \(0,0989098789098767\dots\)
8. \(0,6574839201928374\dots\)
9. \(0,1234567890987654\dots\)
   \(\phantom{0}\vdots\)

Eli yllä olevassa listassa on nyt kaikki desimaaliluvut nollan ja ykkösen väliltä, eikös joo? Okei, nyt teen pienen tempun. Keksin luvun \(x\), jonka desimaalikehitelmä on seuraava: \(x=0,011111111\dots\). Laitoin \(n.\) desimaaliksi ykkösen, jos \(n.\) luvun \(n.\) desimaali oli jotain muuta kuin ykkönen, ja jos se oli ykkönen, laitoin nollan. Eli esimerkiksi jos katsotaan lukua kohdassa 3. Sen kolmas desimaali on kaksi (joka ei ole yksi), joten laitoin \(x\):n kolmosdesimaaliksi ykkösen. Ensimmäisen luvun ensimmäinen desimaali sen sijaan on ykkönen, joten laitoin \(x\):n ensimmäiseksi desimaaliksi nollan.

Okei, mitä hyötyä tästä oli? Minulla on nyt hupsu luku \(x\), jonka \(n.\) desimaali on eri kuin listan \(n.\) luvulla. Siis se ei voi olla yksikään listan luvuista! Se ei ole listan ensimmäinen luku, koska sen ensimmäinen desimaali on eri kuin listan ensimmäisellä luvulla. Se ei voi olla listan toinen luku, koska sen toinen desimaali on eri kuin listan toisella luvulla. Se ei voi olla listan kolmas luku, koska… noh, eiköhän idea jo välittynyt.****

Miten meillä voi olla luku, joka ei ole listassa, jos listassa olivat kaikki luvut? No sehän tarkoittaa, että listassa ei voinut olla kaikkia lukuja. Mikä tahansa lista lukuja annetaankin, tällä tavalla löytyy aina luku, joka ei ollut listassa. Siten mikään lista ei sisällä kaikkia lukuja nollan ja ykkösen väliltä.

Aika hurjaa, tämä jos mikä voi tuntua aluksi epäintuitiiviselta. Tästä voidaan päätellä, että on olemassa ainakin kaksi erikokoista äärettömyyttä. Samanlaisella diagonaaliargumentilla kuin mitä yllä käytettiin voidaan itse asiassa todistaa, että on olemassa ÄÄRETÖN MÄÄRÄ ÄÄRETTÖMYYKSIÄ. Aina löytyy isompi ja isompi ja isompi ääretön joukko. Ehkä paneudun tähän tarkemmin joskus toiste.

Lopuksi voisin vielä todeta, että ei tämä esittämäni bijektioähellys ole ainoa tapa määritellä, mitä tarkoittaa olla ”samankokoinen”. Mielestäni perustelin sen ottamisen määritelmäksi ihan hyvin, mutta joku voisi väittää, että jos meillä on kaksi joukkoa, joista toinen on toisen osajoukko (eli toisen kaikki alkiot ovat myös siinä toisessa joukossa; esimerkiksi luonnolliset luvut ovat kokonaislukujen osajoukko), niin tällöin sen osajoukon pitäisi olla näistä kahdesta pienempi. Tällä tavalla saataisiin erilainen käsitys äärettömyydestä ja mahtavuudesta, mutta väitän, että ei läheskään yhtä hyödyllinen. ”Oikealla” määritelmällä äärettömillä joukoilla on osajoukkoja, jotka ovat yhtä mahtavia kuin joukko itse.

Asiat kuitenkin ovat matematiikassa täysin niin kuin ne matemaatikko haluaa määritellä. Me luomme itse oman maailmamme ja jätämme todellisen maailman tutkimisen niille, jotka sellaisesta enemmän tykkäävät.

* Joskin kisassa vastattiin joka kysymyksessä mukamas todennäköisyys \(p\), joka on vastaajan arvaus todennäköisyydestä, jolla oikea vastaus on ”totta”.
** Oikeasti tästä ”määritelmästä” tulee vakavia ongelmia, mutta niistä ei tarvitse tässä yhteydessä puhua.
*** Jonkun pitäisi tehdä tästä käyttäytymistieteellinen tutkimus. Miten pikkulapsi todellisuudessa todennäköisesti ratkaisi ongelman ”onko turkooseja palloja yhtä paljon kuin punaisia palloja”?
**** Tämä on Georg Cantorin kuuluisa diagonaaliargumentti. Tässä on pieniä teknisiä ongelmia, jotka liittyvät reaalilukujen desimaalikehitelmien yksikäsitteisyyteen, mutta lakaisen ne iloisesti maton alle, koska idea on tärkeämpi kuin tekninen toteutus.